
- 참고 사이트: https://geukggom.tistory.com/8
[C# 기초] #19.Graph - Graph의 정의, 종류, 구현 방법
1. Graph란? 정점(vertex(V))과 그 정점을 연결하는 간선(edge(E)을 하나로 모아 놓은 자료구조. 연결되어 있는 객체 간의 관계를 표현할 수 있는 자료구조입니다. G = (V, E) (ex) 지도, 지하철 노선도, 전기
geukggom.tistory.com

<그래프(Graph)란?>
- 정점(vertex)과 그 정점을 연결하는 간선(edge)을 하나로 모아 놓은 자료구조이다.
- 그래프도 트리와 같이 라이브러리에서 제공되지 않기 때문에 직접 구조를 구현해야 한다.
<그래프의 종류>
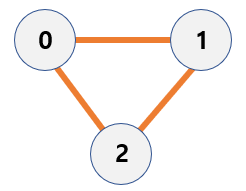
1. 무방향 그래프
: 두 정점을 연결하는 간선에 방향이 없는 그래프. 두 정점 간 양 방향으로 이동 가능.
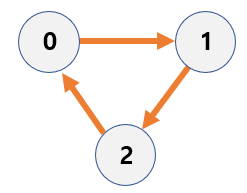
2. 방향 그래프
: 두 정점을 연결하는 간선에 방향이 있는 그래프. 두 정점 간 특정 방향으로만 이동 가능.
3. 가중 그래프
: 정점을 연결하는 간선에 가중치(Weight)가 있는 그래프. 네트워크라고도 함.

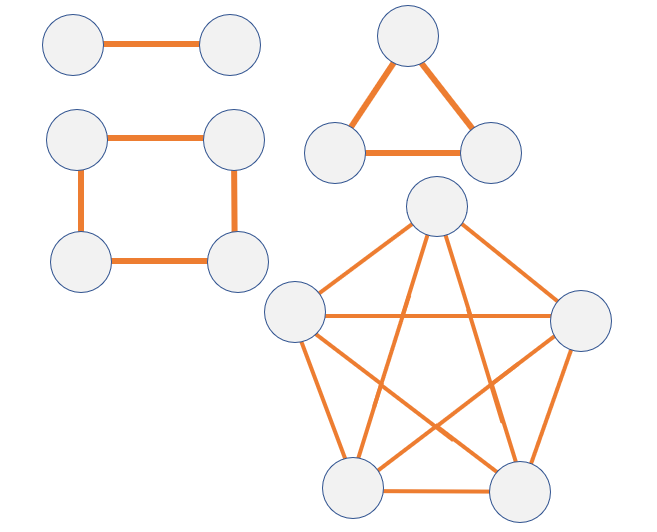
4. 완전 그래프
: 그래프의 모든 정점이 1:1 간선으로 연결된 그래프.
-최대 간선의 수 = (무방향 그래프) n(n-1) / 2, (방향그래프) n(n-1).
-정점의 개수 = n.
<그래프의 구현 방법(인접 행렬, 인접 리스트)>
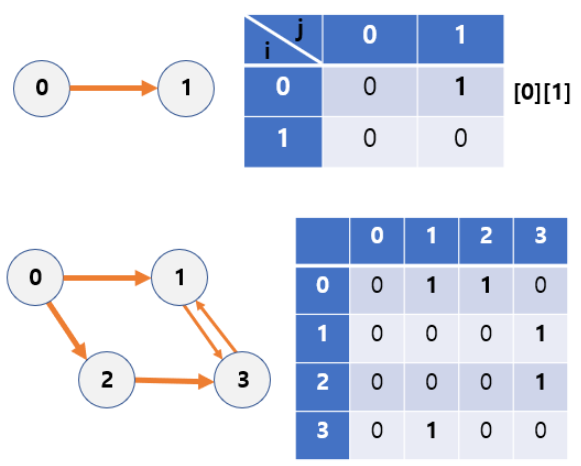
1. 인접 행렬 (Adjacency matrix)
-2차원 배열로 그래프를 표현하는 방식.
-그래프의 정점을 행과 열로 표현하며, 각 인덱스의 데이터는 해당 두 정점 사이의 간선의 존재 여부를 나타냄.
-무방향 그래프의 경우 대칭 행렬이며, 방향 그래프의 경우 대칭이 아닐 수 있음.
-장점
: 두 정점 사이의 간선 존재 여부를 확인하는 것이 빠르고, 새로운 간선을 추가하고 제거하는 것이 빠름.
-단점
: 간선의 개수와 관계없이 배열의 크기가 항상 n x n개이므로 메모리를 많이 잡아 먹음.
노드의 추가 및 제거가 오래 걸림.
모든 간선의 수를 찾기 위해 모든 노드를 순회해야 함.
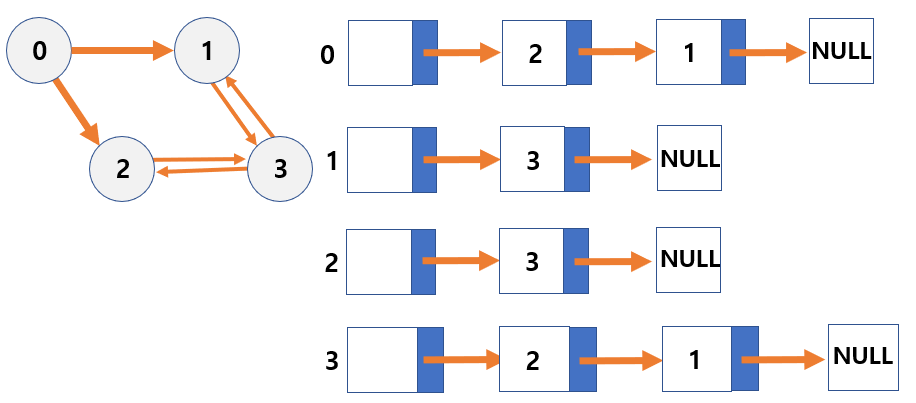
2. 인접 리스트 (Adjacency List)
-각 정점마다 인접한 정점들의 리스트를 저장하는 방식.
-동적 배열이나 연결 리스트로 구현 가능.
-장점
: 간선의 수에 따라 메모리 사용량이 달라지기 때문에 메모리 효율이 좋음.
특정 노드에 직접 접근할 수 있어 인접한 노드를 찾기 쉬움.
노드, 간선의 추가 및 제거가 빠름.
모든 간선의 수를 찾는 것이 빠름
-단점
: 두 정점 사이의 간선 존재 여부를 확인하기 위해 인접 리스트에서 특정 정점의 인접한 정점들을 모두 순회해야 하므로 시간이 더 오래 걸릴 수 있음.
<그래프 구현 코드>
1. 인접 행렬(Adjacency Matrix)
int[,] adjacencyMatrix;
void Start()
{
TestAdjacenctMatrixGraph(4);
}
public void TestAdjacenctMatrixGraph(int lineAndRow)
{
//행과 열.
adjacencyMatrix = new int[lineAndRow, lineAndRow];
//간선 추가 함수에 정점 할당.
for (int i = 0; i < lineAndRow; i++)
{
if (i + 1 == lineAndRow)
{
AddEdge(i, 0);
}
else
{
AddEdge(i, i + 1);
}
}
//간선의 수.
int cntEdge = 0;
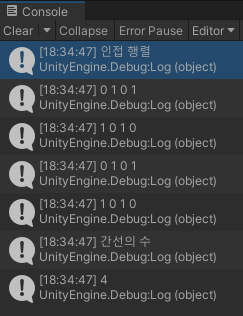
Debug.Log("인접 행렬");
for (int i = 0; i < lineAndRow; i++)
{
string row = "";
for (int k = 0; k < lineAndRow; k++)
{
row += adjacencyMatrix[i, k] + " ";
if (adjacencyMatrix[i, k] == 1)
cntEdge++;
}
Debug.Log(row);
}
//무방향 그래프이기 때문에 나누기 2.
cntEdge = cntEdge / 2;
Debug.Log("간선의 수");
Debug.Log(cntEdge);
}
//간선 추가 함수.
public void AddEdge(int vertex1, int vertex2)
{
adjacencyMatrix[vertex1, vertex2] = 1;
//무방향 그래프일 경우.
adjacencyMatrix[vertex2, vertex1] = 1;
}
2. 인접 리스트(Adjacency List)
List<List<int>> adjacencyList;
void Start()
{
TestAdjacencytListGraph(4);
}
public void TestAdjacencytListGraph(int lineAndRow)
{
adjacencyList = new List<List<int>>(lineAndRow);
for (int i = 0; i < lineAndRow; i++)
{
adjacencyList.Add(new List<int>());
}
for (int i = 0; i < lineAndRow; i++)
{
if (i + 1 == lineAndRow)
{
AddEdge(i, 0);
}
else
{
AddEdge(i, i + 1);
}
}
//간선의 수.
int cntEdge = 0;
//인접 리스트 출력
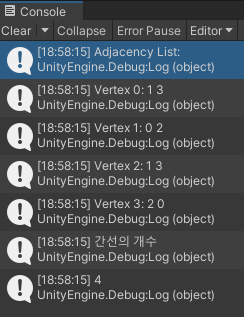
Debug.Log("인접 리스트");
for (int i = 0; i < lineAndRow; i++)
{
string row = "정점 " + i + ": ";
foreach (int neighbor in adjacencyList[i])
{
row += neighbor + " ";
cntEdge++;
}
Debug.Log(row);
}
cntEdge = cntEdge / 2;
Debug.Log("간선의 개수");
Debug.Log(cntEdge);
}
//간선 추가 함수.
public void AddEdge(int vertex1, int vertex2)
{
adjacencyList[vertex1].Add(vertex2);
//무방향 그래프일 경우.
adjacencyList[vertex2].Add(vertex1);
}
'C# > 자료구조 이해하기' 카테고리의 다른 글
| C# 자료구조 트리(Tree)에 대해 알아보자 (0) | 2024.03.26 |
|---|---|
| C# 해시셋(HashSet)에 대해 알아보자! (0) | 2024.03.18 |
| C# object 데이터 타입과 값, 참조 형식을 알아보자! (0) | 2024.03.13 |
| C# 해시테이블(Hash table)에 대해 알아보자! (0) | 2024.03.13 |
| C# 연결리스트(Linked List)에 대해 알아보자! (0) | 2024.03.13 |
