
힙 정렬
- 내림차순을 기준으로 정렬.
- 완전 이진 트리의 일종으로 우선 순위 큐를 위하여 만들어진 자료구조.
- 최댓값, 최솟값을 쉽게 추출할 수 있는 구조.
- 내림차순 정렬을 위해서는 최대 힙을 구성, 오름차순 정렬을 위해서는 최소 힙을 구성하면 됨.
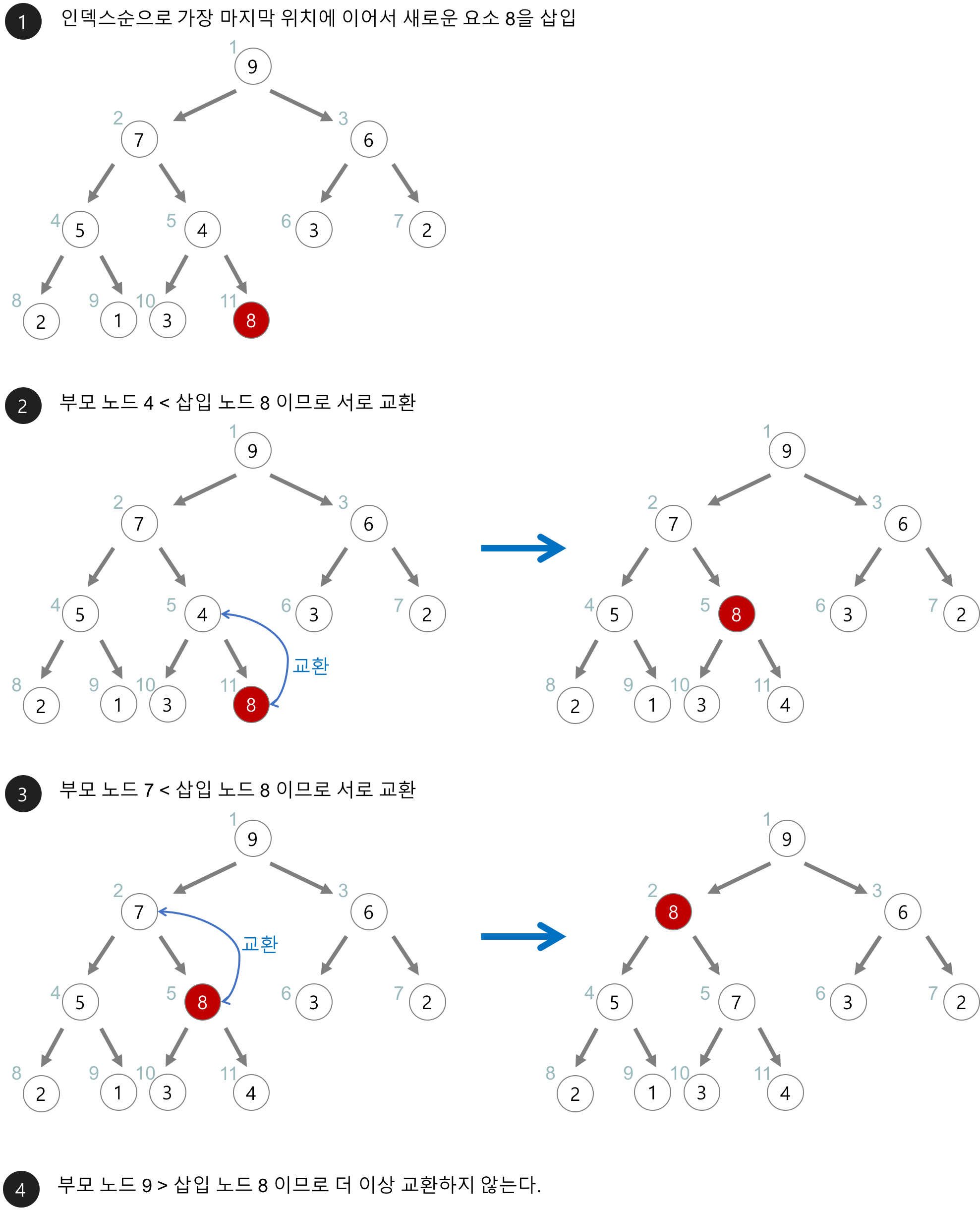
- 배열을 최대 힙으로 만듦(내림차순 정렬).
- 배열의 뒤부터 하나씩 저장.
- 삭제되는 원소들을 순서대로 정렬(오름차순 정렬).
<이미지 출처: https://gmlwjd9405.github.io/images/data-structure-heap/maxheap-insertion.png>
힙 정렬 C# 코드
public void Heap_Sort(List<int> list)
{
for (int i = (list .Count- 1)/2; i >= 0; i++)
{
My_Heap(list, i, list.Count);
}
for (int i = list.Count - 1; i > 0; i++)
{
int temp = list[0];
list[0] = list[i];
list[i] = temp;
My_Heap(list, 0, i);
}
}
public void My_Heap(List<int> list, int rootNum, int maxNum)
{
int root = rootNum;
int left = root * 2 + 1;
int rigth = root * 2 + 2;
if (left < root && list[left] > list[root])
{
root = left;
}
if (rigth < root && list[rigth] > list[root])
{
root = rigth;
}
if(root != rootNum)
{
int swap = list[rootNum];
list[rootNum] = list[root];
list[root] = swap;
My_Heap(list, maxNum, root);
}
}
- 장점
- 시간복잡도가 비교적 좋은 편.
- 힙 정렬 구조가 가장 유용한 경우는 전체 자료의 정렬이 아닌 최댓값 몇 개만 필요할 때임.

<이미지 출처: https://gmlwjd9405.github.io/images/algorithm-heap-sort/sort-time-complexity.png>
'C# > 알고리즘 기초 익히기' 카테고리의 다른 글
| 재귀 알고리즘에 대해 알아보자! (0) | 2024.04.01 |
|---|---|
| 순차탐색과 이진탐색 알고리즘에 대해 알아보자! (0) | 2024.04.01 |
| 병합 정렬(Merge Sort)에 대해 알아보자! (0) | 2024.04.01 |
| 셸 정렬(Shell Sort)에 대해 알아보자! (0) | 2024.04.01 |
| 퀵 정렬(Quick Sort)에 대해 알아보자! (0) | 2024.04.01 |
